안녕하세요, 마인즈앤컴퍼니입니다.
오늘 AI 스터디에서는 Diffusion 모델이 처음 소개된 이후 초기의 복잡성을 단순화하고 속도를 높여 Diffusion 모델의 활용성을 키워준 DDPM과 DDIM이 무엇인지 알아보도록 하겠습니다.
초기 Diffusion 모델이 복잡했던 이유는 복잡한 loss function 수식 때문인데요. 이를 단순화한 방법을 설명하려면 수식에 대한 이해가 필요할 수밖에 없는 부분이 있습니다. 각 모델의 개선점에 초점을 맞추어 최대한 직관적으로 설명해 보았으니 조금은 어렵게 느껴지시더라도, 천천히 따라와주시면 충분히 DDPM과 DDIM을 이해하실 수 있을 거라 생각합니다😊
작성 - 마인즈앤컴퍼니 Data Scientist 조상우 매니저
집/검수 - 마인즈앤컴퍼니 AI Connect 사업부 Data Scientist 이녕민 매니저
DDPM; Denoising Diffusion Probabilistic Models
Diffusion 모델은 크게 Markov assumption과 정규분포를 기반으로 하며, 노이즈를 추가하는 Forward process $q(x_{1:T}|x_0)$와 노이즈를 제거하는 Reverse process $p_\theta(x_{0:T})$ 두 단계로 이루어진 모델입니다.

그리고 Diffusion 모델의 objective 함수를 아래 긴 수식과 같이 표현할 수 있습니다.
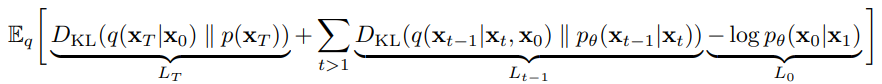
여기서 $L_T$ 는 Forward Process에서, $L_{t-1}$과 $L_0$는 Reverse Process에서 Kullback–Leibler divergence를 최소화하는 방향으로 모델을 학습하게 됩니다. 이때, DDPM 모델은 학습 파라미터들을 부분적으로 상수로 정의함으로써 그 수를 줄여 모델 학습 과정을 단순화합니다.
Forward Process
Forward Process에서 원본 이미지로부터 노이즈를 추가하는 과정은 아래 식을 만족하면서 진행됩니다.
$$ \alpha_t := 1- \beta_t \ \text{ and } \bar{\alpha}_t := \prod_{s=1}^{t} \alpha_s$$
$$ q(x_t | x_{t-1}) := N(x_t; \sqrt{1-\beta_t}x_{t-1}, \beta_t I) $$
여기서 DDPM은 $\beta_1,\dots\beta_T$를 상수로 정의해 Forward Process의 objective 함수인 $L_T$에서도 학습 파라미터가 사라지며 고정값을 가지게 됩니다. 이렇게 크게 loss function의 세 개의 항 중 하나를 상수로 바꾸었습니다.
Reverse Process
Diffusion 모델은 Reverse Process에서도 잠재 변수(latent variable)로부터 이미지를 복원할 때 다음과 같은 식을 따르도록 모델을 학습하게 됩니다.
$$ p_{\theta}(\textbf{x}_{t-1} | \textbf{x}_t) = N(\textbf{x}_{t-1}; \mu_{\theta}(\textbf{x}_t, t), \textstyle{\sum}_{\theta}(\textbf{x}_t, t)) $$
DDPM은 여기서 variance를 아래와 같이 정의합니다.
$$ \textstyle{\sum}_{\theta}(\textbf{x}_t, t) = \sigma_t^2 \textbf{I}, \text{ where } \ \sigma_t^2 = \beta_t \ \text{or} \ \sigma_t^2 = \tilde{\beta}_t$$
이로써 variance는 상수가 되고, 모델은 $p_{\theta}(x_{t-1} | x_t)$ 정규분포의 평균에 해당하는 $\mu_{\theta}(x_t,t)$ 만 학습하게 됨으로써 모델이 학습해야 할 파라미터의 범위를 또 한 번 줄입니다.
그래서 DDPM은…
이렇게 학습 파라미터를 마구 줄여도 괜찮을까, 의문이 드실 수도 있는데요. DDPM 논문에 따르면 아래 그림과 같이 Diffusion 모델의 objective를 단순화해도 기존의 대표적인 이미지 생성 모델인 ProgressiveGAN과 비슷한 성능을 보인다고 합니다.

위에서 설명해 드린 DDPM은 아래의 pseudo-code로 전체 프로세스를 요약할 수 있습니다. 요약하고 보니 굉장히 간단해 보이네요.

DDIM; Denoising Diffusion Implicit Models
Diffusion 모델은 GAN에서 소개한 adversarial training 없이도 이미지를 잘 생성하고, DDPM은 위에서 소개한 방법으로 학습 파라미터를 줄여 개선을 이루어 냈습니다. 하지만 DDPM은 여전히 Markov Chain에 따라 noising/denoising 작업을 진행하게 되고, 그렇기 때문에 매 step을 밟으며 모델을 학습하고 sampling 해야 하므로 여전히 시간이 오래 걸린다는 단점이 있습니다. 이를 해결하기 위해 DDIM 논문이 소개되었습니다.
Forward Process
DDPM의 forward process는 $x_t$가 바로 이전 step 값 $x_{t-1}$에 의해 결정되는 Markovian Chain이지만, DDIM에서는 $x_t$가 바로 이전 step 값인 $x_{t-1}$와 첫 번째 값인 $x_0$에 의해 결정되는 Non-Markovian Chain입니다.

$$ q_{\sigma}(x_t | x_{t-1}, x_0) = \frac{q_{\sigma}(x_{t-1}|x_t, x_0)q_{\sigma}(x_t|x_0)}{q_{\sigma}(x_{t-1}|x_0)} $$
그리고 $\sigma$가 forward process가 얼마나 stochastic한지 조절할 수 있게 되고, $\sigma \rightarrow 0$ 일 때 $x_0,x_t$가 주어지면 $x_{t-1}$은 고정값을 가지게 됩니다.
Reverse Process
DDIM에서 reverse process는 noisy한 $x_t$에서 $x_0$를 예측한 후, 이것과 reverse 조건부 분포 $q_{\sigma}(x_{t-1} | x_t, x_0)$ 활용해 $x_{t-1}$을 구합니다.
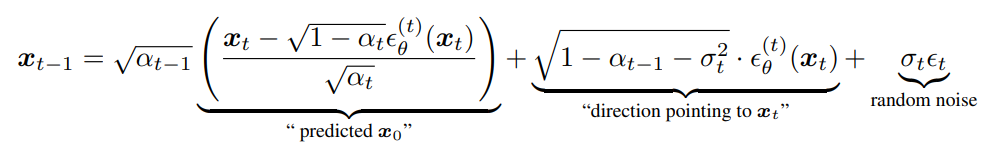
DDIM 논문에서는 이 중 노이즈에 해당하는 부분을 $\sigma_t = \eta \sqrt{(1-\alpha_{t-1})(1-\alpha_t)} \sqrt{(1-\alpha_t/\alpha_{t-1})}$로 표현하여 $\eta = 1$이면 구하고자 하는 objective function이 DDPM의 objective function과 동일하게 되고, $\eta = 0$이면 DDIM 의 objective function이 되게 하였습니다. 이렇게 Reverse Process에서 stochastic한 요소인 랜덤 노이즈를 제외함으로써 DDIM은 동일한 latent space $x_T$에 대해 consistent 한 샘플을 생성할 수 있게 됩니다.

출처: DDIM 논문, 동일한 잠재 변수에 대해 다른 time step에서 샘플링한 이미지 예시
그래서 DDIM은…
DDIM의 가장 큰 변화는 Non-Markovian chain을 따르는 Forward Process와 랜덤 노이즈가 제거된 Reverse Process입니다. 이러한 변화로 인해 모든 time step을 다 밟지 않아도 되기 때문에 DDPM의 샘플링 시간을 단축하려는 목적을 달성할 수 있습니다.
이렇게 진행하는 단계를 줄였다면, 성능 저하는 자연스럽게 따라오는 걱정이겠죠. 하지만 아래 표에서 $\eta=0.0$과 $\eta=1.0$은 각각 DDIM, DDPM 을 의미하는데, 진행한 샘플링 step 수인 S가 특히 작을수록 DDIM의 성능이 더 좋은 것을 볼 수 있습니다. 이때, 논문에서 DDPM Reverse Process 실행 시 더 큰 노이즈 $\hat{\sigma}_t = \sqrt{(1-\alpha_t/\alpha_{t-1})}$을 부여하는데 이는 CIFAR10 데이터셋을 생성하는 데만 이 기법을 활용했다고 하네요. 또한, $S=1000$에서 DDPM의 성능이 더 높은 예외 상황이 발생하긴 하지만, DDIM의 경우가 샘플 수에 따른 성능 개선이 균일한 것을 확인할 수 있습니다.

출처: DDIM 논문, FID 성능 비교
또한, 노이즈가 제거되어 Reverse Process가 deterministic 해진 덕분에 latent space로부터의 interpolation 또한 가능해졌습니다. 아래 그림을 보면, latent space 간의 interpolation이 더 자연스러워진 것을 확인할 수 있습니다.

출처: DDIM 논문, DDIM interpolation 예시
생성 모델 시리즈를 마무리하며
생성 모델의 시대를 이끌고 있는 Diffusion Model의 대표적인 두 논문 DDPM과 DDIM에 대하여 알아보았습니다. 지금은 모두 아시는 것처럼 Stable Diffusion, DALL-E, GLIDE 등 text-to-image 생성 분야만 해도 다양한 모델이 계속해서 소개되고 있을 만큼 그 어느 때보다 빠른 발전을 거듭하고 있는 때죠. 이 시리즈를 통해 생성 모델에 관심을 가지게 되셨다면, 생성 모델을 다양하게 접하기에 가장 좋은 시기인 바로 지금! 조금 더 깊이 있게 생성 모델을 공부하고 또 다양한 인사이트를 나눠주시면 좋겠습니다.
긴 글 함께 해주셔서 감사합니다! 😊🖐️
AI CONNECT에서 생성 모델에 대한 더 많은 경험을 이어가보세요!
Reference
Ho, J. C., Jain, A., & Abbeel, P. (2020). Denoising Diffusion Probabilistic Models. arXiv (Cornell University). https://arxiv.org/pdf/2006.11239.pdf
Song, J., Meng, C., & Ermon, S. (2021). Denoising Diffusion Implicit Models. arXiv (Cornell University) . https://doi.org/10.48550/arxiv.2010.02502