지난 글까지 Regression에 대해 공부했습니다. Regression의 개념과 유형, Regression 모델의 성능을 높이는 데 사용되는 방법, 성능을 측정하는 방식들을 말이죠. 이번 시간부터는 Clustering에 대해 배워볼 예정입니다.
[ML101] #1. Machine Learning? 에서 Machine Learning을 크게 Supervised Learning, Unsupervised Learning, Reinforcement Learning 으로 구분할 수 있다는 내용 기억하시나요?
지난 글까지 살펴본 Regression이 Supervised Learning의 대표적인 모델이었다면 오늘부터 살펴볼 Clustering은 Unsupervised Learning의 대표적인 모델입니다. 말 그대로 데이터가 정답인지 아닌지 Label이 없는 상태에서 유사한 특징을 갖고 있는 데이터 집단(Cluster)으로 구분하는 것을 말합니다.
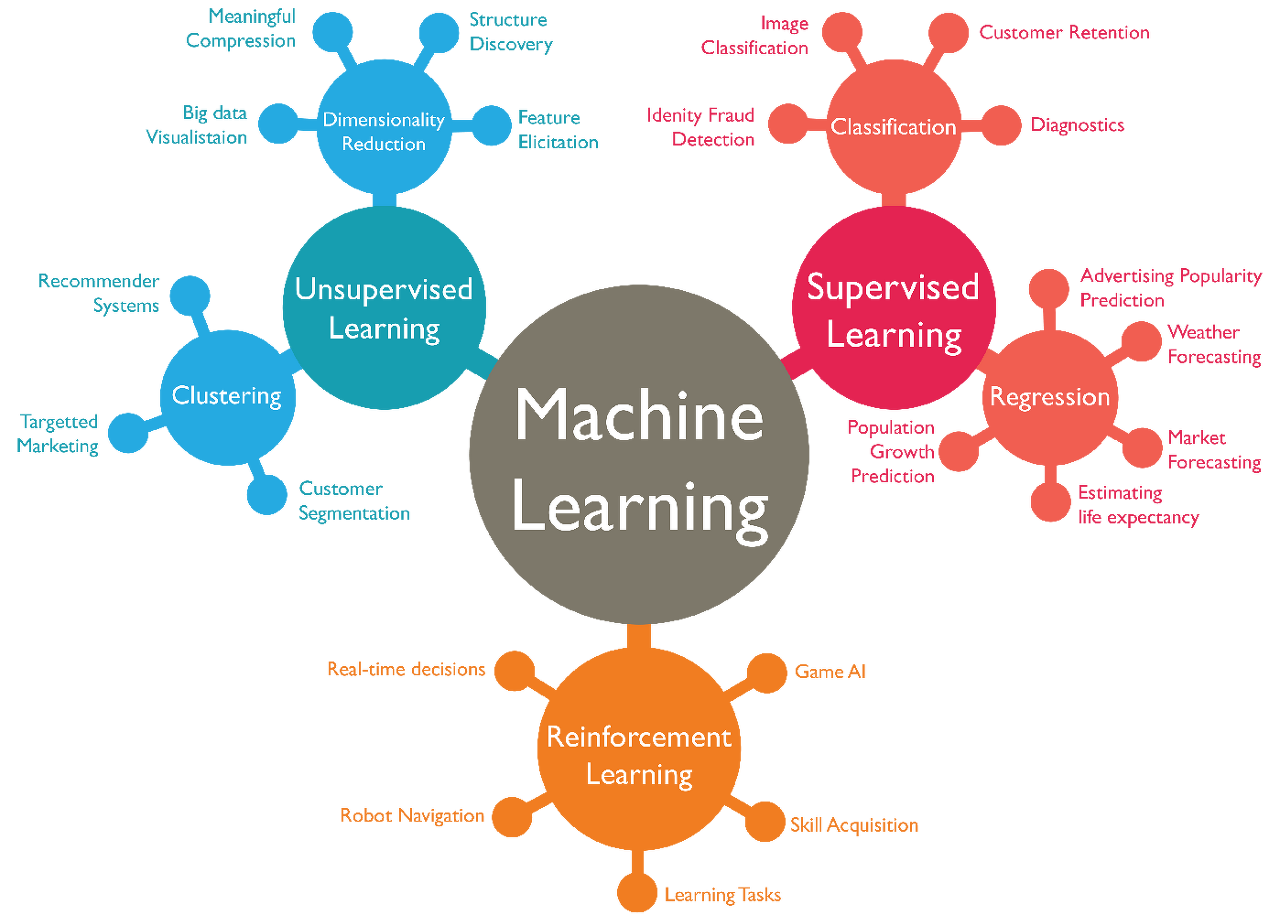
Clustering은 데이터들의 특성을 고려해 유사한 특성을 가진 데이터들을 하나의 집단으로 정의하고 해당 집단의 대표점을 만들어 상호 배타적인 다른 집단과 구별하는 데이터 분석 방법입니다. 전통적인 통계 방법에서도 많이 활용되어 왔고, 다양한 기업에서 타겟 마케팅이나 추천 시스템을 적용하기 위해 고객 Segmentation 분석 등의 Clustering을 적용하고 있습니다. 그럼 지금부터 Clustering의 다양한 유형에 대해 살펴보도록 하겠습니다.
1. 연결 기반 (Connectivity-based) Clustering
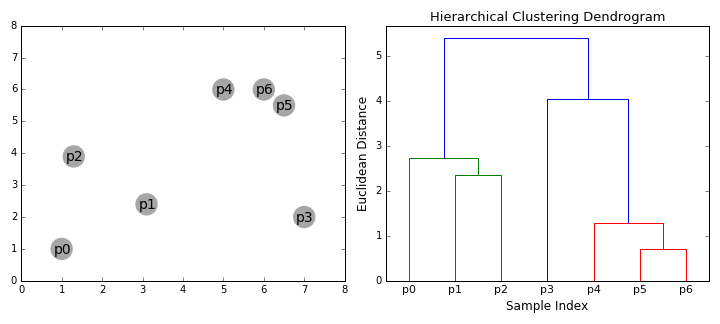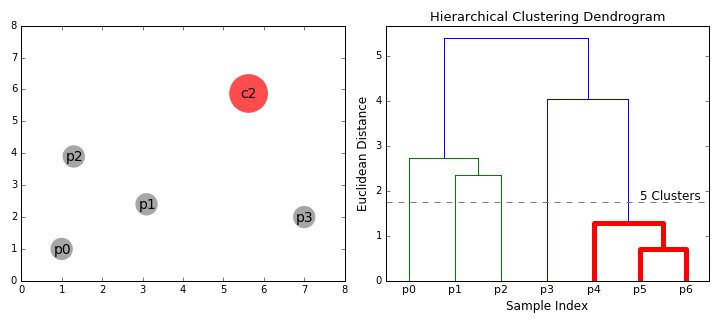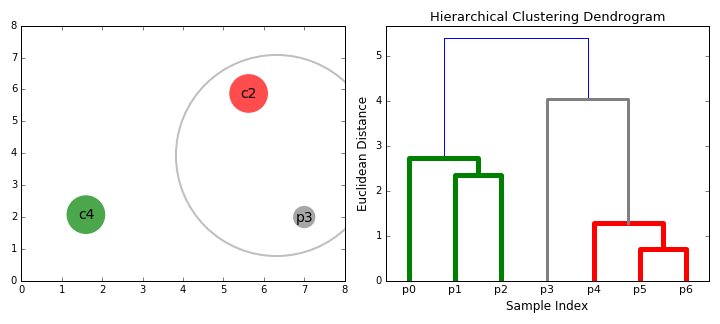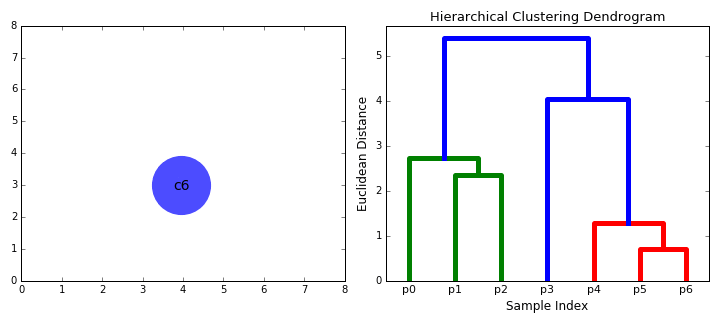
연결 기반 Clustering은 계층적(Hierarchical) Clustering이라고도 합니다. 거리가 가까운 데이터는 유사한 특성이 있을 것이라는 관점으로 가까이 있는 데이터들끼리 순차적으로 집단을 만들어 나가는 것이죠. 거리를 측정한다는 점에서 뒤에 나오는 중심 기반(Centroid-based) Clustering과 유사한 특성이 있지만 집단 내 데이터 간 최대 거리를 기준으로 집단을 구분한다는 점에서 차이가 존재합니다. 집단 내 데이터 간 최대 거리를 얼마로 설정하는지에 따라 아래 그림처럼 집단의 수가 늘어나거나 줄어들 수 있습니다.
연결 기반 Clustering은 직관적으로 해석하기 쉬운 장점이 있습니다. 하지만 데이터 셋에 이상치가 포함될 경우 신규 Cluster가 정의되어 집단의 복잡성이 증가되는 등 확장성이 부족하고 집단을 나누는 기준이 주관적이어서 집단 간 차별적인 특성을 공유하는지에 대한 의문이 생길 수 있습니다.
2. 중심 기반 (Centroid-based) Clustering
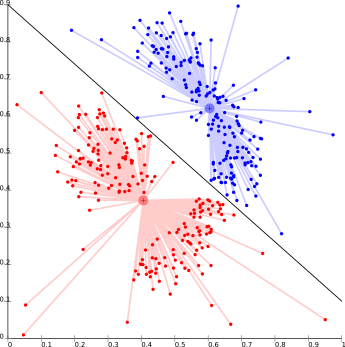
중심 기반 Clustering은 위에서 언급된 계층적 Clustering과 다르게 비계층적 방법입니다. 주어진 데이터 포인트를 반복적으로 Cluster로 만들면서 여러 집단을 만들고 각 집단의 중심으로부터 데이터 포인트의 거리를 계산합니다. 집단 중심에 대한 근접성을 기반으로 한 유사성에 따라 Cluster가 결정되죠. 일반적으로 Cluster의 개수를 사전에 설정하는데 K-means Clustering이 대표적입니다. 사전 정의된 Cluster 개수(K)에 의해 데이터 포인트들이 중심으로부터 거리를 최소화하는 방향으로 Cluster를 형성합니다.
중심 기반 Clustering은 효율적이지만 초기 조건과 데이터 이상치에 민감할 수 밖에 없습니다. Cluster 수를 미리 정의하는만큼 데이터에 대한 사전 지식도 필요합니다. Cluster 수를 미리 알 수 없는 경우 사용하기 힘든 방법이죠. K-means Clustering, Mean-shift Clustering이 중심 기반 Clustering의 대표적인 모델인데, 다음 글에서 자세하게 살펴보도록 하겠습니다.
3. 분포 기반 (Distribution-based) Clustering
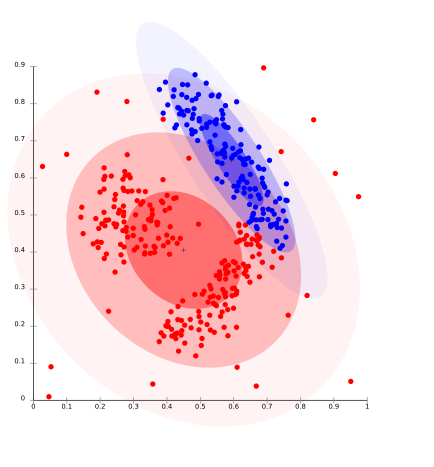
분포 기반 Clustering은 확률에 기반한 유사성으로 Cluster를 나눕니다. 데이터 포인트들이 가우시안 분포(정규 분포의 대표)와 같은 확률분포를 가진다는 가정 하에 데이터가 같은 분포에 속할 수 있는지의 확률로 Cluster를 나누는 방법이죠. 일반적으로 고정된 수의 분포가 생성되고 과적합의 이슈를 해결하기 위해 데이터 분포에 맞게 반복적으로 Cluster를 만들면서 주어진 데이터가 동일한 분포로 묶일 수 있는 Cluster가 만들어 집니다. 분포 중심에서 거리가 멀어짐에 따라 데이터가 분포에 속할 확률도 감소합니다.
분포 기반 Clustering은 복합적인 데이터나 다양한 크기의 Cluster에서 유용합니다. 하지만 데이터의 분포 유형을 모른다면 사용하기 어렵다는 단점이 있습니다. 대표적인 모델인 EM(Expectation-Maximization) Clustering에 대해 다음 글에서 자세하게 살펴보겠습니다.
4. 밀도 기반 (Density-based) Clustering
밀도 기반 Clustering은 데이터 포인트의 밀도를 확인하고 밀도가 높은 영역을 Cluster로 연결하는 방법입니다. 데이터를 다양한 밀도 영역으로 구성하고 서로 다른 밀도 영역을 배타적인 Cluster로 나눕니다. 밀도가 높은 영역이 있으면 새로운 Cluster가 생성되는데 밀도가 높은 영역이 다양하게 펼쳐져 있는 데이터 셋이라면 Cluster 수가 늘어가 복잡성을 증가시킬 수 있습니다. 또한 데이터의 차원이 높을 경우에 적용하기 어렵다는 점, 이상치 데이터를 누락시키는 경우도 존재합니다. 대표적인 모델로는 DBSCAN(Density-Based Spatial Clustering of Applications with Noise)이 있습니다.
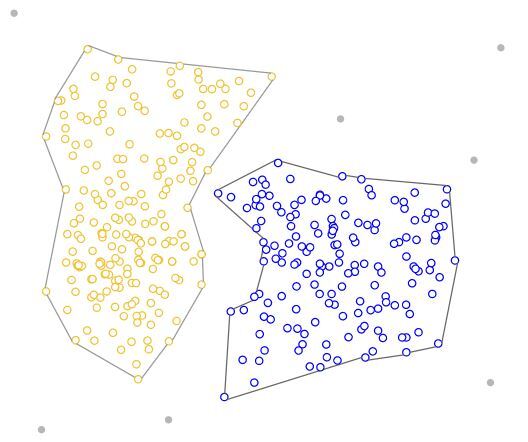
지금까지 Unsupervised Learning의 Clustering 유형에 대해 알아봤습니다. 다음 글에서는 각 유형별 대표적인 모델의 활용 방식과 장단점을 구체적으로 살펴보겠습니다.
'AI Study > ML101' 카테고리의 다른 글
| [ML101]#9. 차원 축소(1) (0) | 2022.04.26 |
|---|---|
| [ML101]#8.Clustering (2) (0) | 2022.04.26 |
| [ML101] #6. Overfitting (0) | 2022.04.26 |
| [ML101] #5. Confusion matrix (0) | 2022.04.26 |
| [ML101] #4. Gradient descent (0) | 2022.04.26 |