[ML101] 시리즈의 세 번째 주제는 경사 하강법(gradient descent)입니다. 지난 시리즈에서 손실 함수(loss function)를 통해 모델의 예측값이 실제값과 차이가 나는 정도, 즉 오차값을 측정하는 방법들을 알아보았습니다.
우리가 가지고 있는 데이터들을 잘 설명할 수 있도록 손실 함수, 비용 함수(loss function, cost function), 또는 목적 함수(objective function)를 이용하여 가장 최적의 모델을 만듭니다. 이 과정은 최적화(optimization)라고도 하는데, 여기에서 사용되는 방법이 경사 하강법입니다.

경사 하강법은 손실함수의 결과값(오차값, 그림의 y축)이 최소값이 되는 최적인 모델의 파라미터 θ(x축)를 찾는 과정입니다. 그림에서 볼 수 있듯이 모델의 파라미터(선형회귀에서는 회귀계수. 즉, 기울기나 절편값)을 바꾸면 정답과의 오차가 바뀝니다. 어떤 파라미터를 가진 모델은 정답지와 비슷하기도 하고, 어떤 파라미터에서는 오차가 매우 커지기도 합니다. 손실함수가 1차 방정식이나 2차 방정식 같이 간단한 형태라면 고등수학에서 배웠던 것처럼 미분방정식을 풀어 미분계수가 0인 지점을 찾아서 간단하게 최소값을 찾을 수 있을 겁니다. 하지만 실제 맞닥뜨리게 되는 손실함수는 대부분 그렇게 간단한 형태가 아니어서 미분방정식을 푸는데 너무 많은 시간이 소요됩니다. 때문에 랜덤한 초기 파라미터값에서 시작해서 조금씩 반복하여 목표를 향해 파라미터를 조정해가는 경사 하강법을 사용합니다.
경사 하강법은 앞이 보이지 않는 안개가 낀 산을 내려가야 하는 상황에서 여러 방향으로 작은 걸음을 내딛으면서 높이가 낮아지는 방향으로 조금씩 움직여가는 것과 같습니다. 산은 손실함수이고, 산의 높이는 오차값, 보폭은 학습률(learning rate)입니다. 보폭이 크면 훨씬 빨리 산을 걸어다닐 수 있겠지만 자칫 가장 낮은 지점을 건너뛰게 될 우려가 있고, 오히려 산의 반대편으로 건너뛰어 엉뚱한 곳으로 가기도 합니다. 반대로 보폭이 작으면 가장 낮은 지점을 건너뛸 확률은 적지만 시간이 너무 오래 걸릴 겁니다. 그렇기 때문에 경사 하강법에서는 적절한 이동 거리, 즉 적절한 학습률을 설정해야 합니다.
이 문제에 대해 조금 더 설명해보면, 손실 함수에는 지역 최소값(local minimum)과 전역 최소값(global minimum)이 있는데, 지역 최소값은 함수의 일부 구간의 최소값이고, 전역 최소값은 전체 구간에서의 최소값입니다. 한 손실 함수의 지역 최소값을 모아놓은 집합이 있다면 이 집합의 최소값이 전역 최소값이라고 할 수 있습니다. 경사 하강법에서 가장 중요한 건 시간을 효율적으로 사용하면서도 지역 최소값을 전역 최소값으로 혼동하는 문제를 피하는 것입니다. 이 목표를 확인하고, 이제부터는 보다 구체적으로 세 가지 종류의 경사 하강법이 어떻게 작동되는지 알아보겠습니다.
1. 배치 경사 하강법(Batch gradient descent)
경사 하강법이 구현되려면 파라미터 θ가 바뀔 때마다 손실함수의 결과값이 얼마나 바뀌는지, 그래디언트 벡터(gradient vector)를 측정해야 합니다. 그래디언트 벡터는 파라미터 θ에 대한 손실함수의 편도함수(partial derivative), 쉽게 말하면 현재 발을 딛고 있는 산의 지점에서의 기울기입니다. 한 걸음을 걸었을 때 경사가 높아진다면 반대 방향으로 가야 할 것이고, 경사가 낮아진다면 그 방향으로 계속 가면 높이가 가장 낮은 지점에 도달할 수 있을 겁니다. 그리고 이 그래디언트 벡터가 아주 작아져서 허용오차 범위 내로 들어올 경우 미분계수가 0인 지점, 즉 최소값에 거의 도달했다고 판단합니다.
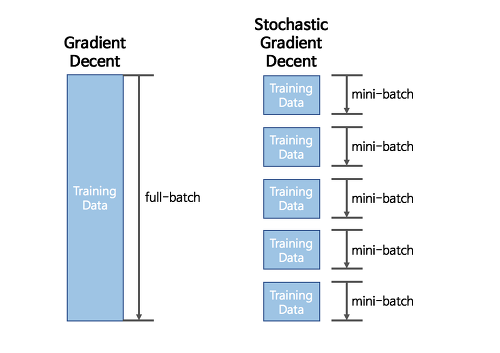
배치 경사 하강법의 가장 큰 특징은 매 스텝에서, 즉 한 걸음 걸을 때마다 모든 데이터의 편도함수를 계산한다는 것입니다. 이 때문에 전체 훈련 세트가 커지면 계산 속도가 매우 느려진다는 단점이 있습니다.
2. 확률적 경사 하강법 (Stochastic gradient descent)
배치 경사 하강법과 정반대로, 확률적 경사 하강법은 매 스텝에서 무작위로 한 개의 데이터를 선택하고, 그 데이터값에 대한 그래디언트 벡터만을 계산합니다. 매 스텝에서 적은 데이터만 처리하기 때문에 배치 경사 하강법에 비해 계산 속도가 월등히 빠르고 전체 훈련 세트의 크기가 크더라도 어렵지 않게 훈련시킬 수 있습니다.
게다가 확률적 경사 하강법은 문자 그대로 ‘확률적’으로, 다시 말해 무작위하게 움직이기 때문에 배치 경사 하강법에 비해 지역 최소값을 피하는 데에는 훨씬 유리합니다. 하지만 전역 최소값이 있는 구간에 들어오고 난 후에는 배치 경사 하강법처럼 엄밀하게 움직이지 않기 때문에 정확한 전역 최소값에 도달하기 어렵다는 단점이 있습니다. 이 딜레마를 해결하기 위해서 초반에는 학습률을 크게 설정해서 지역 최소값에 빠지지 않게 하고, 점진적으로 학습률을 줄여가면서 전역 최소값에 도달하게 하는 방법을 사용하기도 합니다. (learning rate annealing)
3. 미니배치 경사 하강법(Mini-batch gradient descent)
마지막으로 살펴볼 미니배치 경사 하강법은 배치 경사 하강법과 확률적 경사 하강법의 장단점을 종합한 방법으로, 실제로 가장 많이 사용되는 방법입니다. 미니배치 경사 하강법에서는 전체 훈련 데이터셋을 등분한 샘플 세트(미니배치)에 대해 그래디언트 벡터를 계산합니다. 보통 배치사이즈를 8개로 사용한다 등으로 표현하는데, 이는 전체 훈련 데이터셋에서 8개를 한번에 계산하여 최적화하겠다는 의미입니다. 확률적 경사 하강법은 배치 사이즈가 1인 것을 말하기 때문에 많은 이론서에서 미니배치 경사하강법과 확률적 경사 하강법을 혼용해서 쓰기도 합니다.
미니배치 경사 하강법은 배치 경사 하강법보다는 불규칙하고 확률적 경사 하강법보다는 안정적이기 때문에, 배치 경사 하강법보다는 시간이 덜 걸리면서도 확률적 경사 하강법보다 정확한 전역 최소값에 도달할 수 있다는 장점을 가지고 있습니다. 물론 배치 경사 하강법보다는 지역 최소값에서 빠져나오기 힘들고 확률적 경사 하강법보다는 조금 더 시간이 오래 소요된다는 단점도 있기 때문에, 이런 점에 유의해서 세 가지 방법 중 적절한 방법을 선택해야 합니다.
지금까지 경사 하강법에 대해 알아봤습니다. 경사 하강법을 통해 모델을 최적화한 뒤에는 만들어진 모델을 테스트셋를 이용해서 얼마나 정확하게 예측했는지 성능을 평가합니다. 다음 글에서는 정확도를 측정하기 위한 혼동행렬(Confusion matrix)에 대해 더 자세히 알아보겠습니다.
'AI Study > ML101' 카테고리의 다른 글
| [ML101] #6. Overfitting (0) | 2022.04.26 |
|---|---|
| [ML101] #5. Confusion matrix (0) | 2022.04.26 |
| [ML101] #3. Loss Function (0) | 2022.04.26 |
| r[ML101] #2. Regression (0) | 2022.04.26 |
| [ML101] #1. Machine Learning? (0) | 2022.04.26 |