앞의 포스팅에서는 강화학습의 개념을 이해하고, 강화학습을 구성하는 필수 요소들에 대해 알아봤습니다. 이번 포스팅에서는 강화학습 분야에서 오랜 기간동안 연구되어 온 Multi-armed Bandit 문제를 기반으로 Exploration과 Exploitation에 대해 살펴보려고 합니다. Multi-armed Bandit 문제에 대해 설명하고 이 문제를 구현하여 Exploration과 Exploitation 에 대해 설명드리겠습니다.
본 포스팅에서 다루는 설명은 Sutton의 강화학습 책을 많이 참고하였습니다.
관련 코드는 Github 에서 확인할 수 있습니다.
Greedy Method
Exploitation을 하기 위해서 우리는 행동에 대한 평가가 필요합니다. 이 평가는 이전 포스팅에서 배운 Value라는 값을 통해 수행됩니다. Multi-armed Problem에서는 슬롯머신을 선택하는 것을 Action, 특정 슬롯머신을 작동시켰을 때 받는 Reward의 기대값을 Value 라고 할 수 있습니다. 이후 포스팅에서 자세히 살펴보겠지만, Action에 대한 Value 값을 평가하고 수행할 Action을 선택하는 방법들을 Action-value methods 라고 합니다.
Exploitation은 Action에 대한 Value 값을 계산하는 것과 이 Value 값을 이용하여 가장 좋은 Action을 선택하는 것으로 나뉩니다.
Value 값 계산
K-bandit Problem에서 각 슬롯머신의 실제 Value 값을 $q_*(a)$ 라고 하겠습니다. Value 는 Reward의 기대값이므로 각 Action 에 따른 Value 값은 다음과 같이 정의됩니다.
$$q_*(a) \doteq \mathbb{E}[R_t \vert A_t = a]$$
강도는 각 슬롯머신의 내부적인 확률값을 알지 못하기 때문에 $q_*(a)$ 를 예측해야 하며, 직접 경험을 해보는 수밖에 없습니다. 이런 식으로 실제 sampling을 통해 value를 계산하는 방법을 sample average method라고 합니다. 이 예측한 value 값을 $Q$ 라고 하면 다음과 같은 식을 통해 구할 수 있습니다.
$$Q_t(a) \doteq {{\text{sum of rewards when } a \text{ taken prior to } t}\over{\text{number of times } a \text{ taken prior to } t}} = {{\sum^{t-1}_{i=1} R_i \cdot \mathbb{1}_{A_i=a}}\over{\sum^{t-1}_{i=1} \mathbb{1}_{A_i=a}}}$$
여기서 $\mathbb{1}_{A_i=a}$ 는 $t=i$에서 발생한 action이 특정 action과 같으면 1을, 다르면 0을 반환합니다. 특정 Action이 단 한번도 일어나지 않으면 분모는 0이 되기 때문에, 이 경우 value를 0과 같은 특정 값으로 초기화를 해주게 됩니다. 특정 Action이 무한히 많이 선택된다면 $Q_t(a)$ 는 $q_*(a)$ 에 수렴할 것입니다.
Greedy Action
어떤 슬롯머신을 작동시킬 지 선택하는 것은 다양한 방법이 있을 것입니다. 모든 슬롯머신을 한번씩 돌아가면서 실행해보거나, 랜덤으로 선택할 수 있을 것입니다. 만약 현재 상황에서 가장 좋다고 평가한 Action을 구하려면 Value 값인 $Q_t(a)$ 를 최대로 하는 Action을 선택하면 됩니다.
$$A_t \doteq \text{argmax}_{a} Q_t(a)$$
가장 높은 Value의 Action을 선택하는 것을 ‘Greedy’ 하다고 표현하며, 이때 선택된 Action을 Greedy Action, 이러한 방법을 Greedy method라고 합니다.
$\epsilon$-Greedy Method
Greedy method는 현재 상황에서 가장 좋은 Action만을 선택하기 때문에 모든 Value 값을 정확히 알고 있다면 좋은 방법이지만, 초기에는 Value 값을 알지 못하거나 예측한 Value 값에는 Uncertainty가 존재합니다. 이러한 Uncertainty는 Greedy Action을 변경시킬 수 있기 때문에 다양한 Exploration을 통해 Uncertainty를 줄여야 합니다.
Exploitation을 할 때는 가장 좋은 Value 값의 Action을 선택했지만, Exploration은 가장 좋은 행동을 선택하지 않으면 됩니다. 가장 많이 사용하는 방법은 작은 확률인 $\epsilon$ 일 때 Exploration을 하고, 그 이외에는 Exploitation을 하는 것입니다. 이 방법을 $\epsilon$-greedy method 라고 합니다.
Greedy method를 사용하게 되면 단 한번도 선택되지 않는 Action이 존재하기 때문에 초기값으로 남아있는 문제가 존재하지만, $\epsilon$-greedy method을 사용하면 모든 action이 추출되기 때문에 step이 증가할수록 $Q_t(a)$ 는 $q_*(a)$ 에 수렴하게 됩니다. 다만, 문제에 따라 step은 한정되어 있거나 Reward에 대한 Noise 가 심할 수 있습니다. 이러한 문제 때문에 Exploration과 Exploitation의 비중을 어떻게 가져가는 것이 좋을 지 명확히 정하기 어렵다는 문제가 있습니다. 일반적으로 Reward의 값이 변하지 않는다면 time step 이 많을수록, reward의 variance가 클수록 exploration을 많이 하는 것이 좋습니다.
Greedy method와 $\epsilon$-greedy method 의 비교
Agent 의 구현
Agent는 State를 받아서 최적의 Action을 선택해야 합니다. 하지만 Multi-armed bandit에서 State는 1개로 유일하기 때문에 Action을 선택하는 기준은 value 값의 크기로 유일합니다. 또한 Agent는 $\epsilon$ 값에 따라 랜덤한 Action을 선택할 수 있어야 합니다.
아래 코드는 Agent class를 구현한 코드입니다. Agent는 매 time step마다 reward를 저장하여 value를 계산하는 데 사용해야하므로 self.reward_history 라는 Data Frame을 만들었습니다. step 함수는 env class와 $\epsilon$ 값을 받아서, action과 value 값을 반환해줍니다. step 함수에서 $\epsilon$ 값에 따라 Action을 랜덤하게 선택할 지, Greedy 하게 선택할 지 구현하였습니다.
class Agent():
def __init__(self, n_action):
self.n_action = n_action
self.init_values()
def init_values(self):
# 실제 optimal q value 생성
self.pred_q_value_list = [0 for _ in range(self.n_action)]
self.reward_history = pd.DataFrame(columns=['action', 'q_value'])
self.reward_history = self.reward_history.astype({'action':'str', 'q_value':'float'})
def step(self, env, epsilon):
# 한번의 time step 을 진행.
# 1. epsilon 값에 따라 Action 선택 및 reward를 받음
if epsilon > np.random.rand(1):
action = self._get_random_action()
else :
action = self._get_greedy_action()
reward = env.get_reward(action)
# 2. reward_history 에 저장
self.reward_history.loc[len(self.reward_history)] = [str(action), reward]
# 3. 선택된 Action의 Expected Reward 값 (q_value_list)을 업데이트.
self._update_Q_value(action)
def _update_Q_value(self, action):
# 특정 Action에 대한 self.Q_value를 업데이트.
self.pred_q_value_list[action] = self.reward_history[self.reward_history.action == str(action)]['q_value'].mean()
def _get_greedy_action(self):
max_value = np.max(self.pred_q_value_list)
max_actions = np.where(self.pred_q_value_list == max_value)[0]
selected_action = np.random.choice(max_actions)
return selected_action
def _get_random_action(self):
random_action = np.random.randint(self.n_action)
return random_action
Greedy method와 $\epsilon$-greedy method를 비교하기 위해 Optimal value 값을 초기화하고 Agent는 1000번의 time step동안 Reward를 예측합니다. 이러한 일련의 과정을 Episode라고 합니다. 하나의 Episode로는 성능을 비교하기 어렵기 때문에 저는 500번의 Episode를 수행하여 성능을 비교하였습니다.
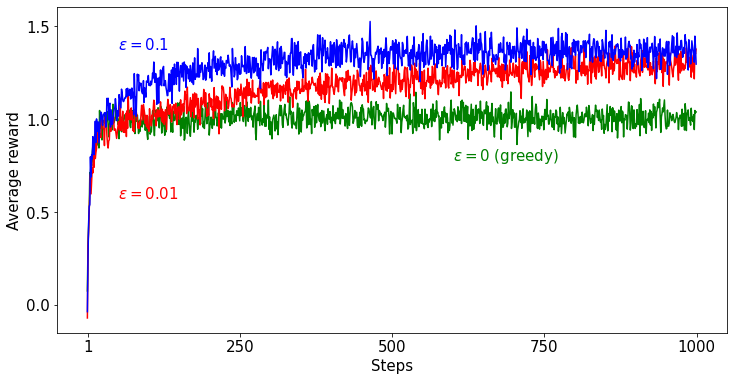
위 그래프는 Greedy method와 $\epsilon$-greedy method를 사용했을 때 모든 Episode의 각 step마다 Reward를 평균한 것입니다. 두 성능을 비교해보면 $\epsilon$ 을 0보다 크게 하여 Exploration을 진행한 것이 Exploitation만 수행한 것보다 성능이 좋은 것을 확인할 수 있습니다. Greedy method가 1.0 정도에 머무르는 것은 Exploitation을 하지 않기 때문에, 초반에 랜덤으로 선택한 슬롯머신의 Reward가 초기값보다 작지만 않으면 같은 슬롯머신을 계속 선택하기 때문입니다.
$\epsilon$ 이 0.1일때와 0.01 일 때를 비교해보면, 0.1일 때가 초반에 더 높은 Reward를 보여주지만 Reward들을 거의 정확히 예측하더라도 10 % 의 확률로 Exploration을 하기 때문입니다. $\epsilon=0.01$ 일 때는 Exploration 확률이 낮아서 Reward들을 정확히 예측하는 데 오래 걸리지만, 정확히 예측하게 되면 1 %의 확률로 Exploitation을 하기 때문에 장기적으로 보았을 때 $\epsilon=0.1$ 보다 Reward가 더 좋아지게 됩니다.

평균적인 Reward 뿐 아니라, Agent가 실제로 가장 Optimal한 Action을 얼마나 많이 선택하는 지 보면 직관적일 것 같습니다. 위의 그래프는 500번의 Episode 동안 1000 번의 Step에서 선택한 Action들이 얼마나 Optimal 한 지 나타낸 그래프입니다.
Greedy method의 경우 어느 하나의 Action이 초기값보다 커지게 되면 그 Action만 선택하기 때문에 Optimal Action을 선택할 확률은 어느정도 step이 지나면 수렴하게 됩니다. $\epsilon$-greedy method의 경우 Exploration으로 인해 시간이 지날수록 Optimal action을 찾게 되며, step 이 길어지게 되면 정확도는 약 $1 - \epsilon$ 으로 수렴하게 됩니다.
Epsilon Decay
앞에서는 Greedy method와 $\epsilon$-greedy method의 성능을 Reward와 Optimal Action을 선택할 확률을 이용하여 비교하였습니다. 그 결과 $\epsilon$ 이 0보다 커서 Exploration을 하는 것이 Value를 예측하는 데 도움이 되며, $\epsilon$ 이 큰 실험에서 Optimal action을 빠르게 찾았습니다. 하지만, 이 $\epsilon$ 값에는 문제가 있는 것 같습니다. 어느정도 정확한 Value를 예측하게 되면 더 이상의 Exploration은 필요가 없습니다. 오히려 랜덤한 Action을 선택하기 때문에 정확한 Action을 할 확률은 1 - $\epsilon$ 의 상한이 생기게 됩니다. 즉, 초반에는 Exploration을 많이 할수록 좋지만, 후반에는 $\epsilon$ 이 0에 수렴할수록 좋은 것이죠. 이러한 이유로 Epsilon Decay 라는 방법을 사용하기도 합니다.
Incremental Implementation
앞에서 살펴본 문제에서는 Action을 수행하면서 관측한 Reward들을 Sampling 하였습니다. 이 Sampling 된 Reward 값들은 Value를 구하기 위해 Data Frame에 계속 저장하였으며, 매 Step마다 history 변수에서 Value를 다시 계산했습니다. 이러한 비효율적인 작업을 없애는 방법은 없을까요? 이전까지 얻은 Reward 값들을 이전 Time step 에서 계산했던 Value 값으로 변환하면 가능합니다.
기존 Sampling 방법으로 Value를 구하던 식을 조금 수정해보면 다음과 같습니다.
$$\begin{align*} Q_{n+1} &= {1 \over n}{\sum^{n}_{i=1} R_i} \\ &= {1 \over n}\Big(R_n + \sum^{n-1}_{i=1} R_i\Big) \\ &= {1 \over n}\Big(R_n + (n-1){1 \over {n-1}} \sum^{n-1}_{i=1} R_i\Big) \\ &= {1 \over n}\Big(R_n + (n-1)Q_n\Big) \\ &= Q_n + {1 \over n}\Big[R_n - Q_n\Big] \end{align*}$$
위 식에서는 $n+1$ 에서의 Value 값을 계산하기 위해 $n$, $Q_n$ 값만 저장하면 됩니다. 이 Update rule을 적용하면 앞 포스팅에서 작성한 Agent Class 코드는 아래 코드와 같이 수정할 수 있습니다.
class Agent():
def __init__(self, n_action):
self.n_action = n_action
self.init_values()
def init_values(self):
# 실제 optimal q value 생성
self.pred_q_value_list = [0 for _ in range(self.n_action)]
self.n_list = [0 for _ in range(self.n_action)]
def step(self, env, epsilon):
# 한번의 time step 을 진행.
# 1. epsilon 값에 따라 Action 선택 및 reward를 받음
if epsilon > np.random.rand(1):
action = self._get_random_action()
else :
action = self._get_greedy_action()
reward = env.get_reward(action)
# 2. n 값 증가
self.n_list[action] = self.n_list[action] + 1
# 3. 선택된 Action의 Expected Reward 값 (q_value_list)을 업데이트.
self.pred_q_value_list[action] = self.pred_q_value_list[action] + (reward - self.pred_q_value_list[action]) / self.n_list[action]
return action, reward
'''
중략
'''
reward를 저장하기 위해 만들었던 self.reward_history 대신 각 Action이 추출된 횟수를 저장하는 self.n_list 를 만들어주고 Action 이 추출될 때마다 1씩 더해주었습니다. step 함수의 마지막에서 더해준 self.n_list 값을 이용하여 $Q$ 값을 업데이트 했습니다.
Update rule을 사용하기 전에는 제 PC에서 500번의 Episode를 계산하는데 약 12분이 걸렸으나, Update rule을 적용했을 때에는 단 20초만에 끝났습니다.
Step Size
위의 Update rule에서, 각 Step에서 실제로 받는 $R_n$ 이 Target 이라 하면 $Q_n$은 기존의 예측값이므로 $R_n-Q_n$ 은 실제 값과 예측값의 차이인 Error 가 됩니다. ${1 \over n}$을 Step size ($\alpha$)라고 하면, 위 식을 더 일반적인 형태로 작성할 수 있습니다.
$$\text{New Estimate} \leftarrow \text{Old Estimate} + \text{Step size} [\text{Target} - \text{Old Estimate} ]$$
기존의 Update rule은 모든 Reward 값들을 동일한 비중으로 보기 때문에 $n$ 이 증가할수록 Error 값에 대한 반영 비중이 낮아집니다. 만약 Optimal value의 값이 특정 값으로 고정되어있는 상황이면 문제가 되지 않으나, Non-stationary 한 상황에서는 최근에 발생한 Reward의 값을 더 크게 보는 것이 합리적입니다. 이것은 Step size 를 특정한 상수 값으로 고정시키면 됩니다. $\alpha$ 를 고정시킨 Update rule 은 이후의 많은 알고리즘에서 사용되기 때문에 매우 중요합니다.
$$Q_{n+1} \leftarrow Q_n + \alpha [R_n - Q_n]$$
Reference
'AI Study > 강화학습' 카테고리의 다른 글
| [RL] 2-1. Exploration과 Exploitation: Multi-armed Bandit Problem (0) | 2022.07.15 |
|---|---|
| [RL] 1-2. 강화학습의 구성 요소 (0) | 2022.04.28 |
| [RL] 1-1. 강화학습이란? (0) | 2022.04.26 |